Optimization with APOSMM

This tutorial demonstrates libEnsemble’s capability to identify multiple minima of simulation output using the built-in APOSMM (Asynchronously Parallel Optimization Solver for finding Multiple Minima) gen_f. In this tutorial, we’ll create a simple simulation sim_f that defines a function with multiple minima, then write a libEnsemble calling script that imports APOSMM and parameterizes it to check for minima over a domain of outputs from our sim_f.

Open in Colab

Six-Hump Camel Simulation Function

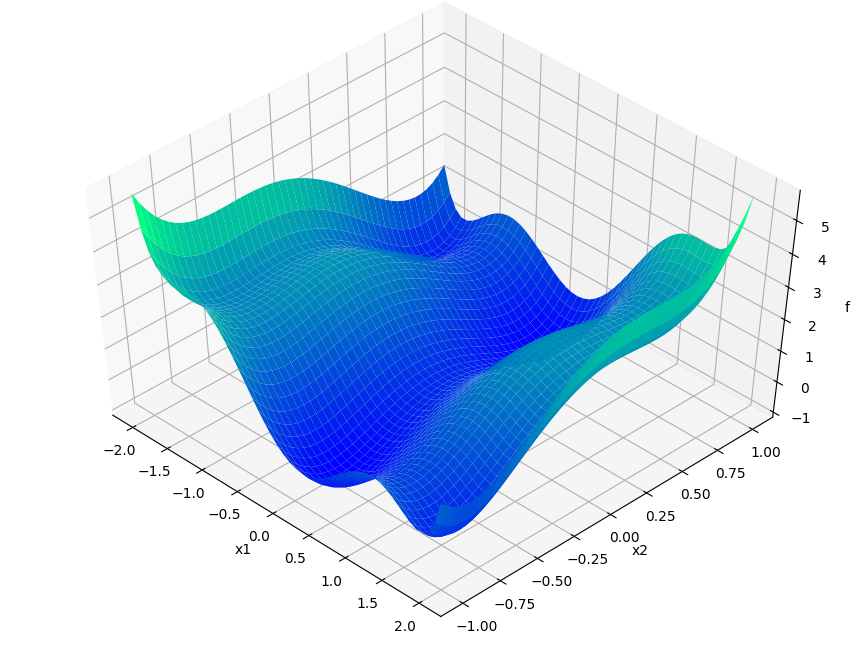
Describing APOSMM’s operations is simpler with a given function on which to depict evaluations. We’ll use the Six-Hump Camel function, known to have six global minima. A sample space of this function, containing all minima, appears below:

Create a new Python file named six_hump_camel.py. This will be our sim_f, incorporating the above function. Write the following:

 1import numpy as np
 2
 3
 4def six_hump_camel(H, _, sim_specs):
 5    """Six-Hump Camel sim_f."""
 6
 7    batch = len(H["x"])  # Num evaluations each sim_f call.
 8    H_o = np.zeros(batch, dtype=sim_specs["out"])  # Define output array H
 9
10    for i, x in enumerate(H["x"]):
11        H_o["f"][i] = six_hump_camel_func(x)  # Function evaluations placed into H
12
13    return H_o
14
15
16def six_hump_camel_func(x):
17    """Six-Hump Camel function definition"""
18    x1 = x[0]
19    x2 = x[1]
20    term1 = (4 - 2.1 * x1**2 + (x1**4) / 3) * x1**2
21    term2 = x1 * x2
22    term3 = (-4 + 4 * x2**2) * x2**2
23
24    return term1 + term2 + term3

APOSMM Operations

APOSMM coordinates multiple local optimization runs starting from a collection of sample points. These local optimization runs occur concurrently, and can incorporate a variety of optimization methods, including from NLopt, PETSc/TAO, SciPy, or other external scripts.

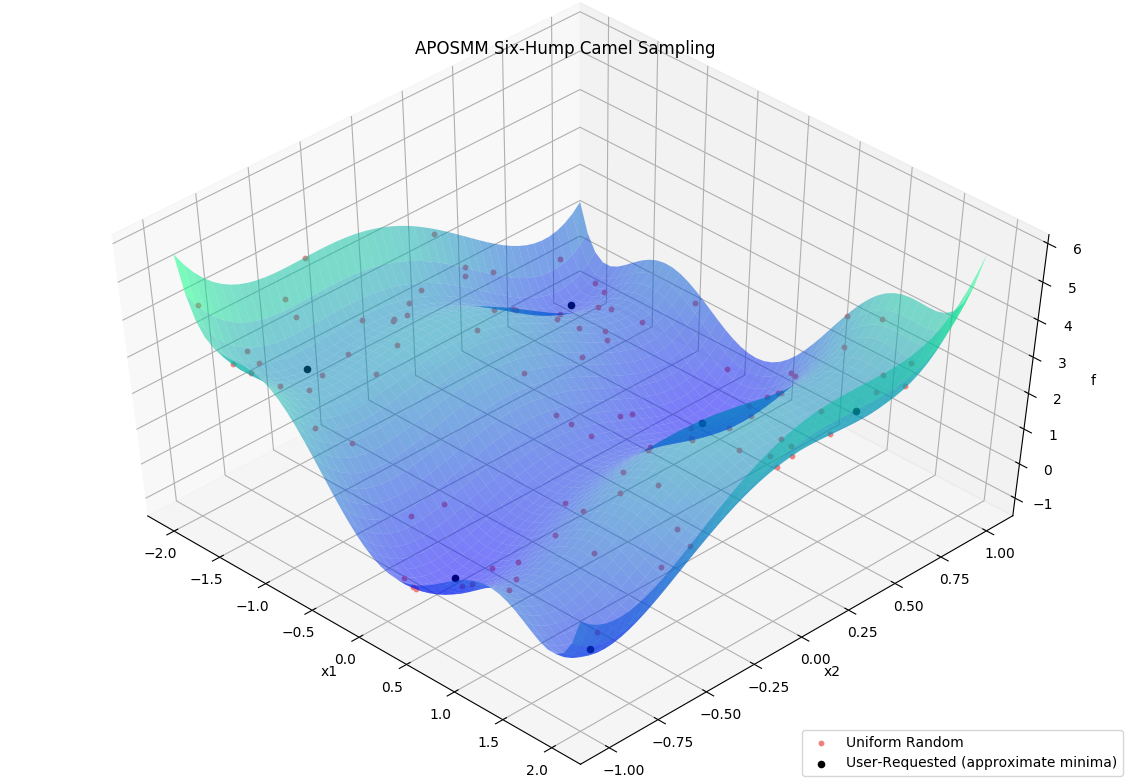
Before APOSMM can start local optimization runs, some number of uniformly sampled points must be evaluated (if no prior simulation evaluations are provided). User-requested sample points can also be provided to APOSMM:

Specifically, APOSMM will begin local optimization runs from evaluated points that don’t have points with smaller function values nearby (within a threshold r_k). For the above example, after APOSMM receives the evaluations of the uniformly sampled points, it will begin at most max_active_runs local optimization runs.

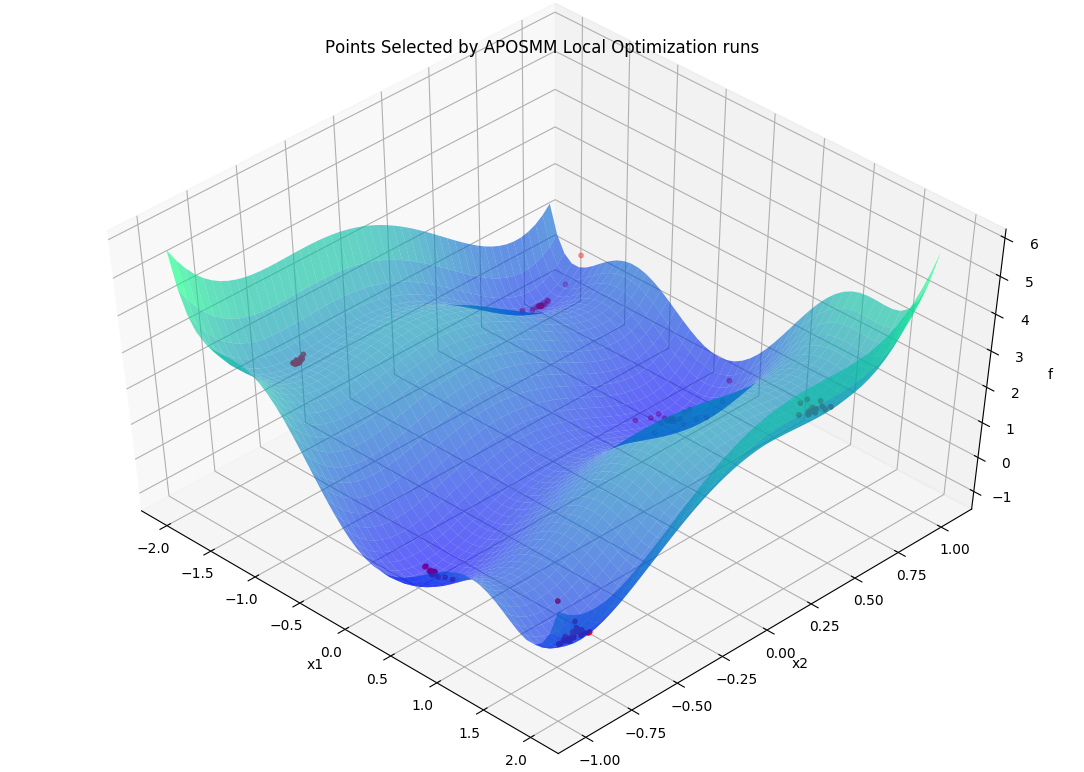
As function values are returned to APOSMM, APOSMM gives them to the corresponding local optimization runs so they can generate the next point(s) in their runs; such points are then returned by APOSMM to the manager to be evaluated by the simulation routine. As runs complete (i.e., a minimum is found, or some termination criteria for the local optimization run is satisfied), additional local optimization runs may be started or additional uniformly sampled points may be evaluated. This continues until a STOP_TAG is sent by the manager, for example when the budget of simulation evaluations has been exhausted, or when a sufficiently “good” simulation output has been observed.

Throughout, generated and evaluated points are appended to the History array, with the field "local_pt" being True if the point is part of a local optimization run, and "local_min" being True if the point has been ruled a local minimum.

APOSMM Persistence

APOSMM is implemented as a Persistent generator. A single worker process initiates APOSMM so that it “persists” the course of a given libEnsemble run.

APOSMM begins its own concurrent optimization runs, each of which independently produces a linear sequence of points trying to find a local minimum. These points are given to workers and evaluated by simulation routines.

If there are more workers than optimization runs at any iteration of the generator, additional random sample points are generated to keep the workers busy.

In practice, since a single worker becomes “persistent” for APOSMM, users should initiate one more worker than the number of parallel simulations:

python my_aposmm_routine.py --comms local --nworkers 4

results in three workers running simulations and one running APSOMM.

If running libEnsemble using mpi4py communications, enough MPI ranks should be given to support libEnsemble’s manager, a persistent worker to run APOSMM, and simulation routines. The following:

mpiexec -n 3 python my_aposmm_routine.py

results in only one worker process to perform simulation evaluations.

Calling Script

Create a new Python file named my_first_aposmm.py. Start by importing NumPy, libEnsemble routines, APOSMM, our sim_f, and a specialized allocation function:

1import numpy as np
2
3from six_hump_camel import six_hump_camel
4
5from libensemble.libE import libE
6from libensemble.gen_funcs.persistent_aposmm import aposmm
7from libensemble.alloc_funcs.persistent_aposmm_alloc import persistent_aposmm_alloc
8from libensemble.tools import parse_args, add_unique_random_streams

This allocation function starts a single Persistent APOSMM routine and provides sim_f output for points requested by APOSMM. Points can be sampled points or points from local optimization runs.

APOSMM supports a wide variety of external optimizers. The following statements set optimizer settings to "scipy" to indicate to APOSMM which optimization method to use, and help prevent unnecessary imports or package installations:

1import libensemble.gen_funcs
2
3libensemble.gen_funcs.rc.aposmm_optimizers = "scipy"

Set up parse_args(), our sim_specs, gen_specs, and alloc_specs:

 1nworkers, is_manager, libE_specs, _ = parse_args()
 2
 3sim_specs = {
 4    "sim_f": six_hump_camel,  # Simulation function
 5    "in": ["x"],  # Accepts "x" values
 6    "out": [("f", float)],  # Returns f(x) values
 7}
 8
 9gen_out = [
10    ("x", float, 2),  # Produces "x" values
11    ("x_on_cube", float, 2),  # "x" values scaled to unit cube
12    ("sim_id", int),  # Produces sim_id's for History array indexing
13    ("local_min", bool),  # Is a point a local minimum?
14    ("local_pt", bool),  # Is a point from a local opt run?
15]
16
17gen_specs = {
18    "gen_f": aposmm,  # APOSMM generator function
19    "persis_in": ["f"] + [n[0] for n in gen_out],
20    "out": gen_out,  # Output defined like above dict
21    "user": {
22        "initial_sample_size": 100,  # Random sample 100 points to start
23        "localopt_method": "scipy_Nelder-Mead",
24        "opt_return_codes": [0],  # Status integers specific to localopt_method
25        "max_active_runs": 6,  # Occur in parallel
26        "lb": np.array([-2, -1]),  # Lower bound of search domain
27        "ub": np.array([2, 1]),  # Upper bound of search domain
28    },
29}
30
31alloc_specs = {"alloc_f": persistent_aposmm_alloc}

gen_specs["user"] fields above that are required for APOSMM are:

  • "lb" - Search domain lower bound

  • "ub" - Search domain upper bound

  • "localopt_method" - Chosen local optimization method

  • "initial_sample_size" - Number of uniformly sampled points generated before local optimization runs.

  • "opt_return_codes" - A list of integers that local optimization methods return when a minimum is detected. SciPy’s Nelder-Mead returns 0, but other methods (not used in this tutorial) return 1.

Also note the following:

  • gen_specs["in"] is empty. For other gen_f’s this defines what fields to give to the gen_f when called, but here APOSMM’s alloc_f defines those fields.

  • "x_on_cube" in gen_specs["out"]. APOSMM works internally on "x" values scaled to the unit cube. To avoid back-and-forth scaling issues, both types of "x"’s are communicated back, even though the simulation will likely use "x" values. (APOSMM performs handshake to ensure that the x_on_cube that was given to be evaluated is the same the one that is given back.)

  • "sim_id" in gen_specs["out"]. APOSMM produces points in its local History array that it will need to update later, and can best reference those points (and avoid a search) if APOSMM produces the IDs itself, instead of libEnsemble.

Other options and configurations for APOSMM can be found in the APOSMM API reference.

Set exit_criteria so libEnsemble knows when to complete, and persis_info for random sampling seeding:

1exit_criteria = {"sim_max": 2000}
2persis_info = add_unique_random_streams({}, nworkers + 1)

Finally, add statements to initiate libEnsemble, and quickly check calculated minima:

1if __name__ == "__main__":  # required by multiprocessing on macOS and windows
2    H, persis_info, flag = libE(sim_specs, gen_specs, exit_criteria, persis_info, alloc_specs, libE_specs)
3
4if is_manager:
5    print("Minima:", H[np.where(H["local_min"])]["x"])

Final Setup, Run, and Output

If you haven’t already, install SciPy so APOSMM can access the required optimization method:

pip install scipy

Finally, run this libEnsemble / APOSMM optimization routine with the following:

python my_first_aposmm.py --comms local --nworkers 4

Please note that one worker will be “persistent” for APOSMM for the duration of the routine.

After a couple seconds, the output should resemble the following:

[0] libensemble.libE (MANAGER_WARNING):
*******************************************************************************
User generator script will be creating sim_id.
Take care to do this sequentially.
Also, any information given back for existing sim_id values will be overwritten!
So everything in gen_specs["out"] should be in gen_specs["in"]!
*******************************************************************************

Minima: [[ 0.08993295 -0.71265804]
 [ 1.70360676 -0.79614982]
 [-1.70368421  0.79606073]
 [-0.08988064  0.71270945]
 [-1.60699361 -0.56859108]
 [ 1.60713962  0.56869567]]

The first section labeled MANAGER_WARNING is a default libEnsemble warning for generator functions that create sim_id’s, like APOSMM. It does not indicate a failure.

The local minima for the Six-Hump Camel simulation function as evaluated by APOSMM with libEnsemble should be listed directly below the warning.

Please see the API reference here for more APOSMM configuration options and other information.

Each of these example files can be found in the repository in examples/tutorials/aposmm.

Applications

APOSMM is not limited to evaluating minima from pure Python simulation functions. Many common libEnsemble use-cases involve using libEnsemble’s MPI Executor to launch user applications with parameters requested by APOSMM, then evaluate their output using APOSMM, and repeat until minima are identified. A currently supported example can be found in libEnsemble’s WarpX Scaling Test.