Calibration with Simulation Cancellation
Introduction - Calibration with libEnsemble and a Regression Model
This tutorial demonstrates libEnsemble’s capability to selectively cancel pending simulations based on instructions from a calibration Generator Function. This capability is desirable, especially when evaluations are expensive, since compute resources may then be more effectively applied toward critical evaluations.
For a somewhat different approach than libEnsemble’s other tutorials, we’ll emphasize the settings, functions, and data fields within the calling script, persistent generator, manager, and sim_f that make this capability possible, rather than outlining a step-by-step process.
The libEnsemble regression test test_persistent_surmise_calib.py demonstrates
cancellation of pending simulations, while the test_persistent_surmise_killsims.py
test demonstrates libEnsemble’s capability to also kill running simulations that
have been marked as cancelled.
Overview of the Calibration Problem
The generator function featured in this tutorial can be found in
gen_funcs/persistent_surmise_calib.py and uses the surmise library for its
calibration surrogate model interface. The surmise library uses the “PCGPwM”
emulation method in this example.
Say there is a computer model \(f(\theta, x)\) to be calibrated. To calibrate is to find some parameter \(\theta_0\) such that \(f(\theta_0, x)\) closely resembles data collected from a physical experiment. For example, a (simple) physical experiment may involve dropping a ball at different heights to study the gravitational constant, and the corresponding computer model could be the set of differential equations that govern the drop. In a case where the computation of the computer model is relatively expensive, we employ a fast surrogate model to approximate the model and to inform good parameters to test next. Here the computer model \(f(\theta, x)\) is accessible only through performing sim_f evaluations.
As a convenience for testing, the observed data values are modelled by calling the sim_f
for the known true theta, which in this case is the center of a unit hypercube. These values
are therefore stored at the start of libEnsemble’s
main History array array, and have associated sim_id’s.
The generator function gen_f then samples an initial batch of parameters
\((\theta_1, \ldots, \theta_n)\) and constructs a surrogate model.
For illustration, the initial batch of evaluations are arranged in the following sense:
The surrogate then generates (suggests) new parameters for sim_f evaluations,
so the number of parameters \(n\) grows as more evaluations are scheduled and performed.
As more evaluations are performed and received by gen_f, the surrogate evolves and
suggests parameters closer to \(\theta_0\) with uncertainty estimates.
The calibration can be terminated when either gen_f determines it has found
\(\theta_0\) with some tolerance in the surrounding uncertainty, or computational
resource runs out. At termination, the generator exits and returns, initiating the
shutdown of the libEnsemble routine.
The following is a pseudocode overview of the generator. Functions directly from
the calibration library used within the generator function have the calib: prefix.
Helper functions defined to improve the data received by the calibration library by
interfacing with libEnsemble have the libE: prefix. All other statements are
workflow logic or persistent generator helper functions like send or receive:
1 libE: calculate observation values and first batch
2 while STOP_signal not received:
3 receive: evaluated points
4 unpack points into 2D Theta x Point structures
5 if new model condition:
6 calib: construct new model
7 else:
8 wait to receive more points
9 if some condition:
10 calib: generate new thetas from model
11 calib: if error threshold reached:
12 exit loop - done
13 send: new points to be evaluated
14 if any sent points must be obviated:
15 libE: mark points with cancel request
16 send: points with cancel request
Point Cancellation Requests and Dedicated Fields
While the generator loops and updates the model based on returned
points from simulations, it detects conditionally if any new Thetas should be generated
from the model, simultaneously evaluating if any pending simulations ought to be
cancelled (“obviated”). If so, the generator then calls cancel_columns():
if select_condition(pending):
new_theta, info = select_next_theta(step_add_theta, cal, emu, pending, n_explore_theta)
...
c_obviate = info["obviatesugg"] # suggested
if len(c_obviate) > 0:
cancel_columns(obs_offset, c_obviate, n_x, pending, ps)
obs_offset is an offset that excludes the observations when mapping points in surmise
data structures to sim_id’s, c_obviate is a selection
of columns to cancel, n_x is the number of x values, and pending is used
to check that points marked for cancellation have not already returned. ps is the
instantiation of the PersistentSupport class that is set up for persistent generators, and
provides an interface for communication with the manager.
Within cancel_columns(), each column in c_obviate is iterated over, and if a
point is pending and thus has not yet been evaluated by a simulation,
its sim_id is appended to a list to be sent to the Manager for cancellation.
Cancellation is requested using the helper function request_cancel_sim_ids provided
by the PersistentSupport class. Each of these helper functions is described
here. The entire cancel_columns() routine is listed below:
def cancel_columns(obs_offset, c, n_x, pending, ps):
"""Cancel columns"""
sim_ids_to_cancel = []
columns = np.unique(c)
for c in columns:
col_offset = c * n_x
for i in range(n_x):
sim_id_cancel = obs_offset + col_offset + i
if pending[i, c]:
sim_ids_to_cancel.append(sim_id_cancel)
pending[i, c] = 0
ps.request_cancel_sim_ids(sim_ids_to_cancel)
In future calls to the allocation function by the manager, points that would have
been distributed for simulation work but are now marked with “cancel_requested” will not
be processed. The manager will send kill signals to workers that are already processing
cancelled points. These signals can be caught and acted on by the user sim_f; otherwise
they will be ignored.
Allocation Function and Cancellation Configuration
The allocation function used in this example is the only_persistent_gens function in the start_only_persistent module. The calling script passes the following specifications:
libE_specs["kill_canceled_sims"] = True
alloc_specs = {
"alloc_f": alloc_f,
"user": {
"init_sample_size": init_sample_size,
"async_return": True,
"active_recv_gen": True,
},
}
async_return tells the allocation function to return results to the generator as soon as they come back from evaluation (once the initial sample is complete).
init_sample_size gives the size of the initial sample that is batch returned to the gen. This is calculated from other parameters in the calling script.
active_recv_gen allows the persistent generator to handle irregular communications (see below).
By default, workers (including persistent workers), are only allocated work when they’re in an idle or non-active state. However, since this generator must asynchronously update its model, the worker running this generator remains in an active receive state, until it becomes non-persistent. This means both the manager and persistent worker (generator in this case) must be prepared for irregular sending/receiving of data.
Calling Script - Reading Results
Within the libEnsemble calling script, once the main libE() function call has returned, it’s a simple enough process to view the History rows that were marked as cancelled:
if __name__ == "__main__": # required by multiprocessing on macOS and windows
H, persis_info, flag = libE(sim_specs, gen_specs,
exit_criteria, persis_info,
alloc_specs=alloc_specs,
libE_specs=libE_specs)
if is_manager:
print("Cancelled sims", H["cancel_requested"])
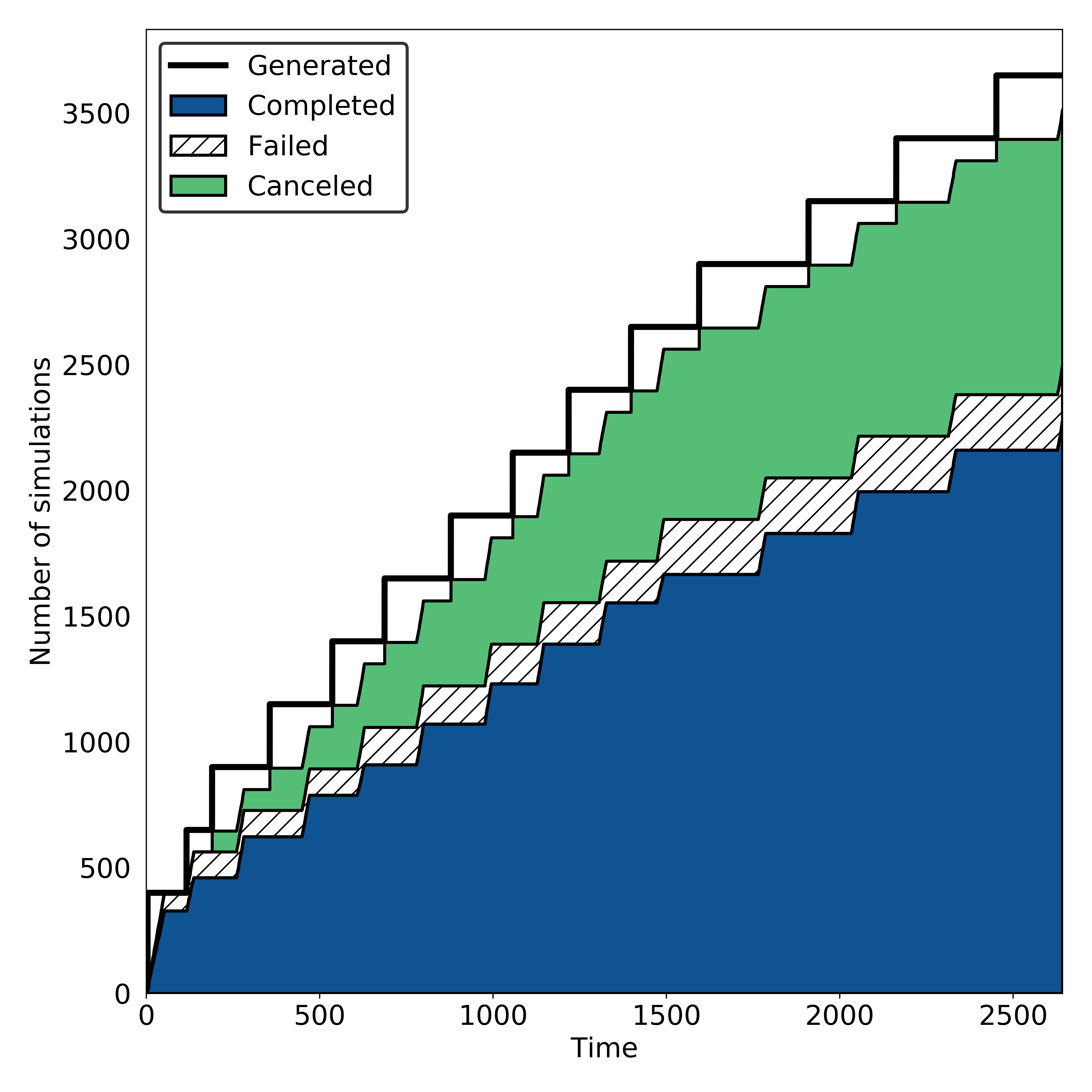
Here’s an example graph showing the relationship between scheduled, cancelled (obviated),
failed, and completed simulations requested by the gen_f. Notice that for each
batch of scheduled simulations, most either complete or fail but the rest are
successfully obviated:
Please see the test_persistent_surmise_calib.py regression test for an example
routine using the surmise calibration generator.
The associated simulation function and allocation function are included in
sim_funcs/surmise_test_function.py and alloc_funcs/start_only_persistent.py respectively.
Using cancellations to kill running simulations
If a generated point is cancelled by the generator before it has been given to a worker for evaluation,
then it will never be given. If it has already returned from the simulation, then results can be returned,
but the cancel_requested field remains as True. However, if the simulation is running when the manager
receives the cancellation request, a kill signal will be sent to the worker. This can be caught and acted upon
by a user function, otherwise it will be ignored. To demonstrate this, the test test_persistent_surmise_killsims.py
captures and processes this signal from the manager.
In order to do this, a compiled version of the borehole function is launched by sim_funcs/borehole_kills.py
via the Executor. As the borehole application used here is serial, we use the
Executor base class rather than the commonly used MPIExecutor
class. The base Executor submit routine simply sub-processes a serial application in-place. After the initial
sample batch of evaluations has been processed, an artificial delay is added to the sub-processed borehole to
allow time to receive the kill signal and terminate the application. Killed simulations will be reported at
the end of the test. As this is dependent on timing, the number of killed simulations will vary between runs.
This test is added simply to demonstrate the killing of running simulations and thus uses a reduced number of evaluations.